De elementen van Euclides · 5342 dagen geleden by Ad van den Ende
Propositions in book I.
1.
a. Construct an equilateral triangle on a given finite straight line.
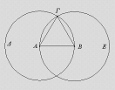
Let AB be the given finite straight line. Which circles will you have to describe?
b. Describe the circles BГΔ with center A and radius AB, and
AГE with center B and radius BA.
Join the straight lines ГA and ГB from the point Г at which the circles cut one another to the points A and B.
Since the point A is the center of the circle BГΔ, therefore AГ equals AB. Again, since the point B is the center of the circle AГE, therefore BГ equals BA. But AГ was proved equal to AB, therefore each of the straight lines AГ and BГ equals AB. And things which equal the same thing also equal one another, therefore AГ also equals BГ.